Magic Cube 4D
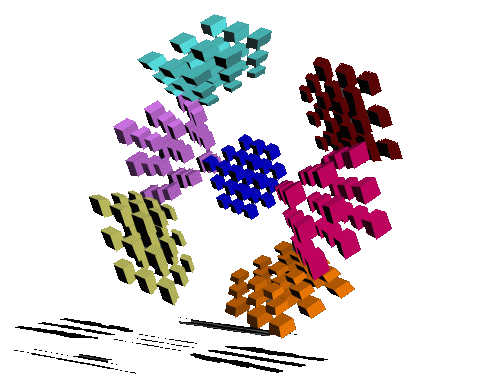
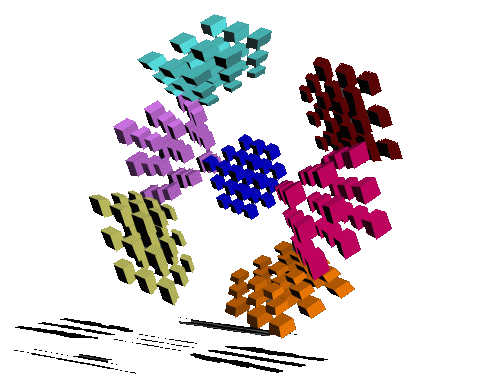
MagicCube4D is a fully functional four-dimensional analog of Rubik's cube plus dozens of other beautiful 4D puzzles. The image above shows the 34 puzzle in its solved state.
or right click here and select "Save link as"
The program is packaged in an executable jar file which should run on any system with a Java virtual machine installed. Save it to your desktop or anywhere you like, so long as you can find it later. Simply double click it to launch; no installation required. On Windows, you can create a desktop shortcut by right-clicking and selecting "Send to > Desktop" from the drop-down. Please read the FAQ for a more complete description of the puzzle. Polish FAQ here. If it doesn't run, you may need to install a current Java virtual machine. Click here for the latest version.
Don Hatch and Melinda Green have developed this puzzle on and off starting in 1988. Jay Berkenbilt and Roice Nelson later joined and made major contributions. Don and Jay were the first to have solved the puzzle making extensive use of macros. Roice was the first person to solve the puzzle without using macros. For his solution he extended Philip Marshall's 3D "Ultimate Solution to Rubik's Cube" into 4D. You can learn Roice's solution if you don't feel like trying to solve it yourself first. Don even wrote a program that can solve Rubik's cubes in any number of dimensions, and created an alternate MC4D implemention. Finally, the Mathologer on YouTube created a solution tutorial that makes solving this puzzle surprisingly straightforward.
At long last, the world's first true physical 4D twisty puzzle! This is a physical version of the 24. Watch the intro video below and visit the project home page to learn more and get one for yourself.
The mathematically inclined may be interested to know that the number of possible states for the 4D cube is exactlywhich can also be expressed as (24!x32!)/2 x 16!/2 x 2^23 x (3!)^31 x 3 x(4!/2)^15 x 4
32! 24! 16! 2^22 6^32 12^15
or in decimal as 1 756 772 880 709 135 843 168 526 079 081 025 059 614 484 630 149 557 651 477 156 021 733 236 798 970 168 550 600 274 887 650 082 354 207 129 600 000 000 000 000
For comparison the normal 3D Rubik's Cube has only 43 252 003 274 489 856 000 unique positions which is still huge. On the other hand the 4D cube has more potential positions than the total number of atoms in the universe! Far more. Talk about a needle in a cosmic haystack! Click the following link to learn how to calculate 4D cube permutations. Surprisingly even though the number of 4D cube positions is frighteningly large this doesn't mean this puzzle is that many times harder to solve. If you can already solve the 3D cube then you're more than half way to solving this one. All the techniques you already know will apply here as well.
Roice wrote a paper describing many of the above puzzles and the way they exploaded from the original Rubik's cube. It was accepted as the cover article in the April 2018 edition of the journal Math Horizons.
Freeware, attribution requested, ideally including links to this page.