copyright 07/06/2002
Wendy Krieger
 |
6664-all.png copyright 07/06/2002 Wendy Krieger |
 |

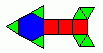
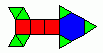
Several different figures can have the same vertex figure. Here, all the figures have a vertex figure of three hexagons and a square, but there are one, two or three hexagons sandwiched between the pairs of squares. We make use of a degenerate 2-gon to represent where a face is possible, but not forming in this instance. Such a polygon arises naturally in symmetry studies. Figure A shows a 6664_1, a figure whith one hexagon between the squares. This is a kind of extended snub. There are three 'different' faces around the hexagon, which are cycled a,b,c,a,b,c. In this case, a=b=2, c=3. Marek would call this the 'antiprismal' 6664.
Figure B shows a 6664_2, which is Marek's snub, which he calls the 6,6,6,4 hexaconfiguration, but this is really a reflected snub process. The hexagons form the snub facets, and the pattern of faces around the snub are a,b,a,c,b,c. In this case, a=b=2, c=4. Marek calls this the hexaconfig 6664.
Figure C shows a 6664_3, which has a Wythoff figure 4 6 | 3. This one a hexagons that have only hexagonal neighbours. Marek calls this the semiregular 6664.
The square can be replaced by any other shape, like a pentagon or a triangle. If it is replaced by a 2-gon, the three processes are the three different ways that the edges of a hexagonal lattice {6,3} can be coloured so that there is a red, blue and green edge at each vertex.
Case A is done with all red edges parallel, all green edges parallel, and all blue edges parallel. The order of edges around the hexagons are then rbgrbg.
Case B is unusual. In essence, all the red edges are parallel as in case 1. But now, a line that is parallel to the red edges passes through only blue lines, or only through green lines.
Case C is based on the usual three-colour colouring of the hexagon plane, in red, blue and green. Here, a red edge lies between a blue and green hexagon, and the hexagons have as edges rbrbrb, bgbgbg, grgrgr.
back to Gallery index
back to Tyler Applet
back to Geometry index
back to Superliminal home