apeirored.png copyright 08/18/2002 Wendy Krieger

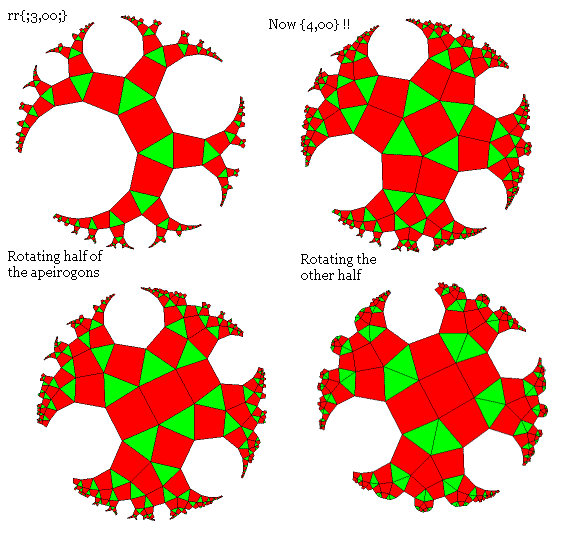
This sequence shows development from the rr{;3,oo;}. The tyler setting here is 4,3,4,0.

The first is the rr{;3,oo;}. Like any rr{;3,p;}, the combination of the {p}-gon, and a layer of triangles and squares, gives a {2p}-gon. Here, p is infinity, and for all intents and purposes, p=2p.

The second figure shows what happens when a 90-degree rotation is applied to one of the squares - here, the one in the centre. It has now strangely lost its original {3,oo} symmetry, and acquired a new, {4,oo} symmetry. The thing can be regarded as a t{;oo;4} with each of the apeirogon-faces capped with a cupola.

The next figure shows half of the apeirogons rotated by one side. There are now lines of three squares, and the overall symmetry is that of an {oo,oo}.

The final frame shows what happens when the second half are rotated. The original rr{;3,oo;} in the first frame disappears, and we are left with something with alternating crosses of squares, and diamonds of triangles.

back to Gallery index
back to Tyler Applet
back to Geometry index
back to Superliminal home