5
SQUARES
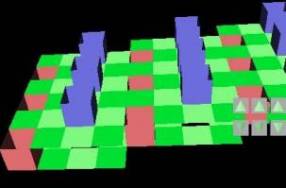
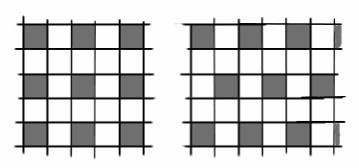
A plane
consist of squares. Remove one square from each vertex (removed squares
are
black). The most obvious solution is given on the left below. It is possible to move the horizontal rows
with black squares one step or the vertical columns with black squares
one
step. If one makes the decision to move at least one horizontal row
then no
vertical column can be moved. Of course
other horizontal rows can moved one step.
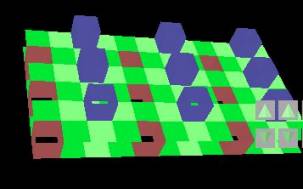
{4,5} 10
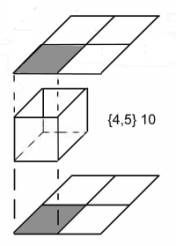An elementary cell, or repeat unit, consists of
an array of 4 squares (1 removed, black),
a cube with the bottom and the top
removed on the black square, and on top an array of 4 squares (1
removed,
black).
In total
3+4+3 = 10 squares.
There are
two different ways to tile this cell into an infinite regular
polyhedron. I.e. two different
sets of translation vectors shown below.
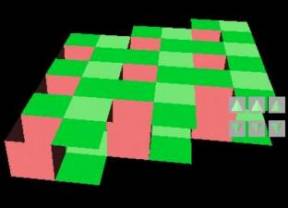
{4,5} 20
This elementary
cell consists of an array of 8
squares (2 removed, black), a cube with the bottom and the top removed
on one
of the black square, an array of 8
squares (2 removed, black) and a cube without top and bottom on the
other
square. In total 6+4+6+4 = 20 squares.
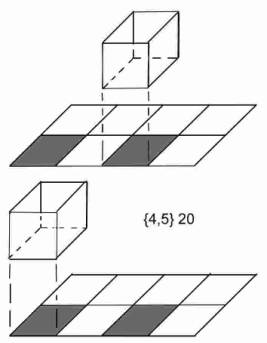
{4,5} 20
This elementary
cell consists of an array of 8 squares (2 removed, black) in a somewhat
different situation.
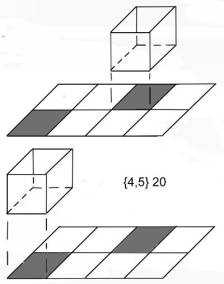
There are
two tilings of this cell shown below.
