Infinite Regular Polyhedra

Polyhedra are surfaces composed of polygons such that each edge is adjacent
to two polygons (or "faces"). Regular polyhedra are those that are composed
of only one type of regular polygon (regular polygons have all edge lengths
and angles equal). Polyhedra that close on themselves have a finite number
of faces, but it's possible to describe polyhedra constructions that are
infinite. In other words, it would take an infinite number of polygons
to complete such a figure which would then fill all of space with a latticework.
Of course an infinite physical model cannot be completely constructed,
but large enough sections can be built to show their geometry and prove
their existence. Here are some 2D and 3D
photographs of some physical models.
The drawing above (courtesy of Steve Dutch) show portions of one such figure with identical vertices each surrounded by six squares. Click the links in the table below for images and 3D models of several more. The famous mathematician H.S.M. Coxeter calls these figures "skew polyhedrons" while J. Richard Gott, III calls them "Pseudopolyhedrons". I'll call them "Infinite Polyhedra", and when they are composed only of regular polygons, I'll call them "Infinite Regular Polyhedra" or simply "IRPs". Regular polyhedra are often represented with a notation called Schläfli symbols which consist of two numbers between curly braces. The first number is the number of sides on each polygon, and the second is the number of such polygons surrounding each vertex (i.e. corner). For example, {4,3} is the cube because each vertex is surrounded by three squares. It's perfectly natural to apply this notation to infinite polyhedra too.
At first it appears that finite and infinite polyhedra are very different sorts of beasts but it turns out that mathematically they can be looked at in very much the same way through the concept of surface "genus". The powerful idea of applying the concept of genus to IRPs may not be new, but the following description and table was recently developed by Lasse Winquist of Sweden.
The genus of a surface is a measure of it's complexity. Any surface that can be smoothly deformed into a simple sphere has a genus of 0. The simplest shape that a coffee cup can be deformed into is a torus (a doughnut shape) which has genus 1. A piece of swiss cheese with many tunnels through it has a genus equal to the number of tunnels.
Euler first discovered the formula F-E+V = 2-2g which relates the number of faces, edges and vertices of a polyhedron to it's genus. At first glance this formula seems to say that the genus of any infinite polyhedron must also be infinite. That even seems natural since IRPs have an infinite number of tunnels. This view is misleading however. A much more powerful application of Euler's formula to infinite polyhedra is to apply it to a minimal repeat unit which can be used to create each IRP. Repeat units are familiar to crystallographers who describe different crystal structures in terms of small clusters of atoms which are arrayed in different ways in three dimensions much like the ways bricks can be arrayed in two dimensions. This method is also useful and natural when describing infinite polyhedra. Imagine a minimal repeat unit of an IRP which has the topology of the following figure:

Any IRP with the topology of the figure above will satisfy these equations only when g=2. Now imagine a repeat unit with the topology of the figure below:

Cosmologists even argue whether the universe itself is really infinite or whether space repeats itself in exactly this way. See the cover article in Scientific American's April 1999 issue for an excellent description of this issue. If this is true, then space itself may have exactly the same shape as is needed to describe some IRPs. Another good reference is a web page by one of the authors of that article which he devoted to describing such tiled spaces via familiar games you can play in such tiled spaces.
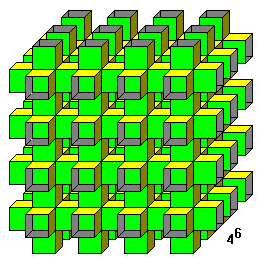
Perhaps the simplist IRP with genus 3 can be generated from a packing of cubes. Click the following link to view models and a description of that {4,6}. For an example of an infinite polyhedron of very high genus, click the following link to view one with genus = 6 w hich can be generated from a packing of rhombic dodecahedra.
The following table lists the number of faces in the repeat units of regular polyhedra. The blue cells represent the finite regular polyhedra, and the purple cells represent infinite regular polyhedra. The yellow cells represent the flat plane tilings which are a sort of degenerate class of polyhedra which sit exactly on the border of the finite and infinite regular polyhedra.
The underlined table entries are links to pages that contain photos
and descriptions of individual IRPs as well as links to VRML models of
those IRP's which can be interactively rotated, scaled, and tiled in
three dimensions. The interactive tiling ability was programmed by
Vladimir Bulatov.
It is currently known to work with the free
Cortona VRML browser plug-in from Parallel Graphics.
Vladimir Bulatov:
images and interactive
models of some IRPs
Steve Dutch, "Hyperbolic Tessellations"
images and descriptions of some more
IRPs by Steve Dutch
and still
more he took from Wells below.
J. R. Gott, "Pseudopolyhedrons", American Mathematical Monthly,
Vol 74, p. 497, 1967.
Illustrates a number of infinite polyhedra
constructed
of regular polygons.
Chaim Goodman-Strauss
and
John Sullivan
Enumerated some of the infinite {4,5} and {4,6}
classes of IRPs which they call
"Hamiltonian in the cubic lattice"
Slavik Jablan "Fullerenes on
other Surfaces"
Mentions the possibilities for
infinite 3D Fullerenes.
A. Wachman, M. Burt, and M. Kleinmann,
Infinite Polyhedra, Technion, Haifa, 1974.
A. F. Wells, "Three-Dimensional Nets and Polyhedra", Wiley, 1977.
Monograph on infinite polyhedra and space
structures,
with a crystallographic perspective.