Möbius Deltahedra
Copyright 1998 Peter Messer

Five non-convex deltahedra which share special symmetry properties

A deltahedron is a polyhedron with faces that are all equilateral triangles. There are an infinite number of non-convex deltahedra and only eight convex deltahedra. The convex set includes three familiar polyhedra: the regular tetrahedron, the regular octahedron, and the regular icosahedron. The eight convex deltahedra are commonly described in general published works on polyhedra [1].
We direct our attention to a unique set of five highly symmetric non-convex deltahedra which appear in the above image of six figures rendered by Rolf Asmund. The last figure in the bottom row represents a "stellated cube" (more technically an equilateral tetrakis hexahedron) which has a similar origin as the others but, as you will see later, it does not satisfy the special symmetry requirements of the other five cases. The symmetry relationships that distinguish our five cases evoke both mathematical interest and esthetic pleasure. Clicking on a figure in the image gives you a VRML display of it which you can rotate and examine in three dimensions. If you do not have a VRML plug-in viewer, you can obtain the free Cosmo 2.0 VRML viewer originally from SGI, though I can't vouch for the above site. The VRML models were created by Melinda Green using the coordinate data generated by Peter Messer. You can easily assemble physical models of these figures by using rigid equilateral triangles made of cardboard or plastic. As you shall see shortly, the pieces do not fall so easily into place if you are attempting an exact mathematical solution. Study each of the figures, look for similarities in symmetry, and make your conclusions before reading on.
The five deltahedra are characterized by the following concise definition:
A deltahedron where each face is bounded by a Möbius triangle of the same symmetry kind.George Hart's excellent page for images and descriptions of the subject. Möbius triangles (2 3 p) are right spherical triangles which have dihedral angles p / 2, p / 3, p / p and which are the fundamental domains for the three polyhedral symmetry groups. In decreasing order they are icosahedral symmetry (2 3 5), octahedral symmetry (2 3 4), and tetrahedral symmetry (2 3 3). Instead of p radians, you may substitute 180 degrees. The sides of Möbius triangles participate as reflection (mirror) planes in the corresponding symmetry group. Each polyhedral symmetry group has a characteristic number of Möbius triangles which are connected in a tessellating pattern that covers a sphere. An excellent introduction that illustrates these triangle reflection units is found in reference [2]. Excluded from our discussion is dihedral symmetry (2 2 p).
Our definition states that each equilateral triangle face fits precisely the same way inside the smallest space (Möbius triangle) bounded by three mirror planes of the deltahedron's symmetry group. Like a kaleidoscope, you can generate the entire figure by sequentially reflecting the images of a given face across the sides of a single Möbius triangle. These mirror planes are not actually visible in the figures. You will note that the mirror planes include only the sides of the equilateral triangles, that is, they do not cut across the interior of the triangles. The top row of Asmund's image shows two figures with icosahedral symmetry. Each is associated with 15 mirror planes. The middle row shows two figures with octahedral symmetry. Each is associated with 9 mirror planes. The first figure of the bottom row shows tetrahedral symmetry which is associated with 6 mirror planes. Intersections of the mirror planes occur in sets of 2, 3, or p mirror planes. These lines of intersections correspond to the rotation axes of the symmetry group, that is, 2-fold, 3-fold, and p-fold rotation, respectively. Each of three vertices of an equilateral triangle lies on a rotation axis of a different kind. The number of Möbius triangles that cover the sphere is known to be 120, 48, and 24for the decreasing polyhedral symmetry groups. Consequently, the rows in the image are associated with 120, 48, and 24 faces, respectively.
It should now be clear that other highly symmetric deltahedra (e.g. tetrahedron, octahedron, icosahedron) do not satisfy our concise definition because they contain mirror planes that cut across the faces.
It turns out that none of the five special deltahedra can be constructed using Euclidean tools (straightedge and compass). This is attributed to the following conditions for generating the equilateral triangle faces. First, fix one vertex of a general (scalene) triangle on a rotation axis of the symmetry group. You are left with two other triangle vertices that slide simultaneously and independently along their respective axes until the distances between all three vertices are the same. You will quickly encounter three simultaneous non-linear equations as you attempt to calculate any of the metrical properties of these deltahedra. By eliminating variables you are at best left with a fourth degree polynomial equation in the desired metrical variable. The polynomial equation is observed to generate two imaginary roots and two real roots in these cases. The real roots turn out to be complicated expressions involving cubic radicals. That is why you see two non-constructible cases with octahedral symmetry and two non-constructible cases with icosahedral symmetry. However, one of the two real roots associated with the tetrahedral symmetry group consists only of square root radicals which of course is constructible. This constructible case appears as a stellated cube which, surprisingly, has full octahedral symmetry. How did this one case start with conditions of tetrahedral symmetry but then end up with octahedral symmetry?
Recall that the tetrahedral Möbius triangle is a right isosceles spherical triangle with angles p / 2, p/ 3, p / 3. Consider one of the 24 transformable triangle faces enclosed by such a right isosceles spherical triangle. Fix one vertex on the 2-fold axis and slide the other two vertices on their respective 3-fold rotation axes. Imagine an equilateral triangle face that ends up with the two sliding vertices being equidistant from the deltahedron's center. The bilateral symmetry of the equilateral triangle relative to the tetrahedral Möbius triangle implies that a new mirror plane must now be added that bisects this equilateral triangle. Overall there are 3 new mirror planes in the deltahedron for a total of 9 mirror planes which fit octahedral symmetry. These are in fact the conditions that occur when the stellated cube is generated under initial tetrahedral symmetry. Because faces are cut by mirror planes, the stellated cube is excluded from our defined set of deltahedra.
We shall now solve a set of equilateral triangle vertices {V2, V3, V5} for each of the two cases of deltahedra with 120 faces. You should then be able to apply similar methods to the remaining special deltahedra with 48 or 24 faces.
Calculations are simplified if we properly orient the set of 120 icosahedral Möbius triangles in a Cartesian coordinate system. We do this by selecting the following placement of the three rotation axes that belong to one icosahedral Möbius triangle. We put the center of the deltahedron at the origin (0, 0, 0) so that
the 2-fold rotation axis coincides with the Z-axis and directed Z > 0,
the 3-fold rotation axis lies in the YZ-plane and directed Y > 0, Z > 0,
the 5-fold rotation axis lies in the XZ-plane and directed X > 0, Z > 0.
We further simplify by using the golden ratio ![]() and assigning the "sliding factors" j along the 3-fold axis and kalong the 5-fold axis. Triangle vertex V2 on the 2-fold axis is conveniently fixed at (0, 0, 1) which lies unit distance from the origin. Triangle vertex V3which slides on the 3-fold axis has general coordinates (0, j/t, jt). Triangle vertex V5 which slides on the 5-fold axis has general coordinates (k, 0, kt). The general coordinates are left for the reader to confirm.
and assigning the "sliding factors" j along the 3-fold axis and kalong the 5-fold axis. Triangle vertex V2 on the 2-fold axis is conveniently fixed at (0, 0, 1) which lies unit distance from the origin. Triangle vertex V3which slides on the 3-fold axis has general coordinates (0, j/t, jt). Triangle vertex V5 which slides on the 5-fold axis has general coordinates (k, 0, kt). The general coordinates are left for the reader to confirm.
Applying the formula in analytic geometry for the distance between two points and then equating the squares of the lengths of the sides of equilateral triangle V2V3V5, we arrive at the relation
![]() from which three simultaneous non-linear equations can be derived. Any two of such equations are sufficient for solving the factors j and k. At this point you must use standard iterative numerical methods for solving simultaneous non-linear equations. You will find two solution sets for j and k which then can be substituted in the general set of vertices noted above.
from which three simultaneous non-linear equations can be derived. Any two of such equations are sufficient for solving the factors j and k. At this point you must use standard iterative numerical methods for solving simultaneous non-linear equations. You will find two solution sets for j and k which then can be substituted in the general set of vertices noted above.
The disadvantage of solving simultaneous equations is that you must estimate starting values for j and k. It is often better to find a polynomial equation in one variable. With a symbolic processor like Mathematica it is easy to generate a fourth degree polynomial equation in j. Next, an expression for k in terms of j would nicely bypass the need for solving a second polynomial equation in k. The desired two equations are
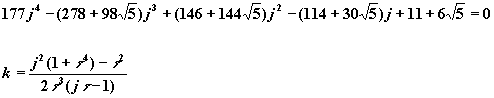 A fourth degree polynomial equation in j can be solved algebraically without initial guesses. Unfortunately the two real roots are very complicated expressions involving cubic radicals and so they are not shown here.
A fourth degree polynomial equation in j can be solved algebraically without initial guesses. Unfortunately the two real roots are very complicated expressions involving cubic radicals and so they are not shown here.
However, expressed in decimal form the two solution sets { j, k} are {0.316383241, 0.44300155} and {1.37056825, 1.17639464} for the first and second case of the 120-faced deltahedron, respectively.
Finally, the equilateral triangle vertices {V2, V3, V5} for the first and second case are approximately
{ {0, 0, 1}, {0, 0.19553559, 0.51191883}, {0.44300155, 0, 0.71679157} }
and
{ {0, 0, 1}, {0, 0.84705776, 2.21762601}, {1.17639464, 0, 1.90344651} }
We succeeded in defining an initial face for both cases of the 120-faced deltahedron. Because the deltahedra have a specific orientation in a Cartesian coordinate system, the other 119 faces can be mapped by applying sequential transformations (rotations, reflections) under icosahedral symmetry.
References
1. Pugh, A. (1976). Polyhedra: A Visual Approach. University of California Press.
2. Wenninger, M.J. (1979). Spherical Models. Cambridge University Press.